Calculus Videos: Differentiation

Video Lectures

Displaying all 58 video lectures.
Lecture 1
Basic Derivative Formulas (Part 1)
Play Video		 Basic Derivative Formulas (Part 1)
Lecture 2
Basic Derivative Formulas (Part 2)
Play Video		 Basic Derivative Formulas (Part 2)
Lecture 3
Sketching the Derivative of a Function
Play Video		 Sketching the Derivative of a Function
Lecture 4
Equation of a Tangent Line
Play Video		 Equation of a Tangent Line
Lecture 5
Linearization at a Point
Play Video		 Linearization at a Point
Lecture 6
Finding the Derivative Using Its Definition
Play Video		 Finding the Derivative Using Its Definition
Lecture 7
Product Rule (1/2)
Play Video		 Product Rule (1/2)
Lecture 8
Product Rule (2/2)
Play Video		 Product Rule (2/2)
Lecture 9
Quotient Rule (1/2)
Play Video		 Quotient Rule (1/2)
Lecture 10
Quotient Rule (2/2)
Play Video		 Quotient Rule (2/2)
Lecture 11
Derivatives Using the Chain Rule (Part 1)
Play Video		 Derivatives Using the Chain Rule (Part 1)
Lecture 12
Derivatives Using the Chain Rule (Part 2)
Play Video		 Derivatives Using the Chain Rule (Part 2)
Lecture 13
Chain Rule: Harder (Ex. 1)
Play Video		 Chain Rule: Harder (Ex. 1)
Lecture 14
Chain Rule: Harder (Ex. 2)
Play Video		 Chain Rule: Harder (Ex. 2)
Lecture 15
Chain Rule: Harder (Ex. 3)
Play Video		 Chain Rule: Harder (Ex. 3)
Lecture 16
More Complicated Derivative Examples (Part 1)
Play Video		 More Complicated Derivative Examples (Part 1)
Lecture 17
Image Not Available
Play Video		 More Complicated Derivative Examples (Part 2)
Lecture 18
Using the Product and Chain Rule to Find a Derivative: Then Factoring and Simplifying
Play Video		 Using the Product and Chain Rule to Find a Derivative: Then Factoring and Simplifying
Lecture 19
Derivatives Using Implicit Differentiation (Part 1)
Play Video		 Derivatives Using Implicit Differentiation (Part 1)
Lecture 20
Derivatives Using Implicit Differentiation (Part 2)
Play Video		 Derivatives Using Implicit Differentiation (Part 2)
Lecture 21
Derivatives Using Implicit Differentiation (Part 3)
Play Video		 Derivatives Using Implicit Differentiation (Part 3)
Lecture 22
Related Rates Problems and Implicit Differentiation
Play Video		 Related Rates Problems and Implicit Differentiation
Lecture 23
Related Rates Involving a Cone
Play Video		 Related Rates Involving a Cone
Lecture 24
Related Rates: A Point Moving on a Graph
Play Video		 Related Rates: A Point Moving on a Graph
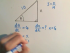
Lecture 25
Related Rates: With Trigonometry
Play Video		 Related Rates: With Trigonometry
Lecture 26
Related Rates: Baseball Diamond Example
Play Video		 Related Rates: Baseball Diamond Example
Lecture 27
Image Not Available
Play Video		 Logarithmic Differentiation (Part 1)
Lecture 28
Logarithmic Differentiation (Part 2)
Play Video		 Logarithmic Differentiation (Part 2)
Lecture 29
Image Not Available
Play Video		 Derivatives Involving Logarithmic Functions: ln(x), log (x), etc.
Lecture 30
Image Not Available
Play Video		 Properties of Logarithms: Functions
Lecture 31
Derivatives Involving Exponential Functions: e^x, a^x, etc
Play Video		 Derivatives Involving Exponential Functions: e^x, a^x, etc
Lecture 32
Image Not Available
Play Video		 Derivatives Involving Inverse Trigonometric Functions
Lecture 33
Inverse Trigonometric Derivative: Example 1
Play Video		 Inverse Trigonometric Derivative: Example 1
Lecture 34
Inverse Trigonometric Derivative: Example 2
Play Video		 Inverse Trigonometric Derivative: Example 2
Lecture 35
Inverse Trigonometric Derivative: Example 3
Play Video		 Inverse Trigonometric Derivative: Example 3
Lecture 36
Inverse Trigonometric Derivative: Example 4
Play Video		 Inverse Trigonometric Derivative: Example 4
Lecture 37
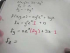
Finding Partial Derivatives
Play Video		 Finding Partial Derivatives
Lecture 38
The General Chain Rule (Part 1)
Play Video		 The General Chain Rule (Part 1)
Lecture 39
The General Chain Rule (Part 2)
Play Video		 The General Chain Rule (Part 2)
Lecture 40
Newton's Method
Play Video		 Newton's Method
Lecture 41
Image Not Available
Play Video		 Where a Function is Increasing and Decreasing, Finding Local Max and Local Min
Lecture 42
Increasing/Decreasing, Local Maximums/Minimums
Play Video		 Increasing/Decreasing, Local Maximums/Minimums
Lecture 43
Finding Critical Numbers (Part 1)
Play Video		 Finding Critical Numbers (Part 1)
Lecture 44
Finding Critical Numbers (Part 2)
Play Video		 Finding Critical Numbers (Part 2)
Lecture 45
First Derivative Test (Part 2)
Play Video		 First Derivative Test (Part 2)


Using the First Derivative to find where a function is Increasing/Decreasing and where the local Maximums and Minimums occur. There are two basic examples.
Lecture 46
Image Not Available
Play Video		 First Derivative Test (Part 2)


Using the First Derivative to find where a function is Increasing/Decreasing and where the local Maximums and Minimums occur. There are harder examples in this lesson.
Lecture 47
Lagrange Multipliers: Finding Max or Min
Play Video		 Lagrange Multipliers: Finding Max or Min
Lecture 48
Using the Second Derivative to Find Local Max and Min
Play Video		 Using the Second Derivative to Find Local Max and Min
Lecture 49
Using the Second Derivative to Find Where a Function is Concave Up/Concave Down
Play Video		 Using the Second Derivative to Find Where a Function is Concave Up/Concave Down
Lecture 50
Optimization Problem (Part 1)
Play Video		 Optimization Problem (Part 1)
Lecture 51
Optimization Problem (Part 2)
Play Video		 Optimization Problem (Part 2)
Lecture 52
Optimization Problem (Part 3)
Play Video		 Optimization Problem (Part 3)
Lecture 53
Finding Local Max, Min and Saddle Points (Part 1)
Play Video		 Finding Local Max, Min and Saddle Points (Part 1)
Lecture 54
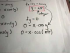
Finding Local Max, Min and Saddle Points (Part 2)
Play Video		 Finding Local Max, Min and Saddle Points (Part 2)
Lecture 55
Curve Sketching Using Calculus: (Part 1 of 2)
Play Video		 Curve Sketching Using Calculus: (Part 1 of 2)


In this video, Patrick discusses the following topics to help produce the graph of a function: domain, x-y intercepts, symmetry of the function, intervals of increase/decrease, local maximums and minimums, concavity, inflection points, and horizontal and vertical asymptotes.
Lecture 56
Curve Sketching Using Calculus (Part 2 of 2)
Play Video		 Curve Sketching Using Calculus (Part 2 of 2)


In this video, Patrick discusses the following topics to help produce the graph of a function: Domain, x-y Intercepts, Symmetry of the Function, Intervals of Increase/Decrease, Local Maximums and Minimums, Concavity, Inflection Points, and Horizontal and Vertical Asymptotes.
Lecture 57
Directional Derivatives
Play Video		 Directional Derivatives


In this video, Patrick gives the formula and does an example of finding the Directional Derivative that corresponds to a given angle.
Lecture 58
Differentials and Approximations
Play Video		 Differentials and Approximations


In this video, Patrick shows the basic idea of Differentials and shows how they can be used to Approximate Values.